Adrien Foucart, PhD in biomedical engineering.
Get sparse and irregular email updates by subscribing to https://adfoucart.substack.com. This website is guaranteed 100% human-written, ad-free and tracker-free.
Our comment article Comments on "MoNuSAC2020: A Multi-Organ Nuclei Segmentation and Classification Challenge" was just published in the April 2022 issue of the IEEE Transactions on Medical Imaging, alongside the author's reply. The whole story is, in my opinion, a very interesting example of things that can go wrong with digital pathology challenges, and of some weaknesses of the scientific publication industry. But let's start from the beginning...
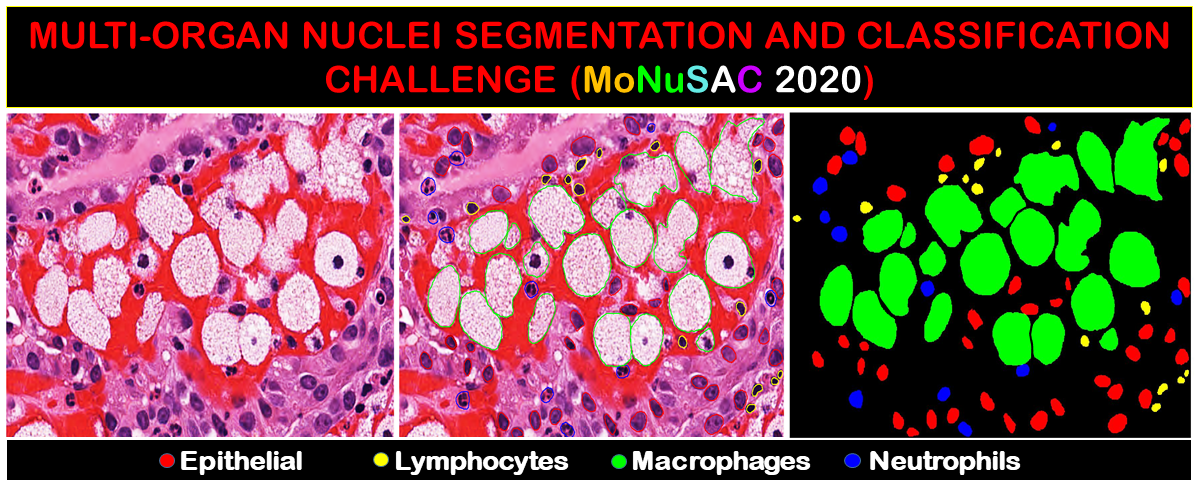
MoNuSAC was a nuclei detection, segmentation and classification challenge hosted at the ISBI 2020 conference. The challenge results were posted online, and a post-challenge paper was published in the IEEE Transactions on Medical Imaging [1] (available in "Early Access" on June 4th, 2021, and published in December 2021). Challenge organisers also published ground truth annotations for the test set, as well as a "colour-coded predictions" on the test set of four of the top-five teams (the link for the L1 team pointing to the predictions of the PL2 team), and the evaluation code used to score the participants' submissions.
In September 2021, as I was working on an analysis of the Panoptic Quality metric [2] used in the challenge, I discovered a bug in the evaluation code and alerted the organisers on September 20th, 2021. They initially replied that "[t]he code to compute PQ is correct". After verification, I confirmed the error and sent a Jupyter Notebook demonstrating it in action.
As I was trying to assess the potential effects of the error on the challenge results, I discovered several additional issues in the evaluation process. On September 22, 2021, I sent a detailed report to the organisers explaining the different problems and offering to "collaborate with [them] in making a correction to the published results". I received no response.
On October 12th, 2021, my PhD supervisor Prof. Decaestecker contacted the managing editor of the IEEE Transactions on Medical Imaging to ask what the procedure was for submitting "comment articles" to the journal, as it seemed to be the preferred method in IEEE journals for reporting potential errors in published papers. After some back-and-forth to clarify the procedure, we submitted our comment article on October 20th, 2021. The comment article was transmitted to the original authors. On February 23rd, 2022, we received notice from the editor-in-chief that our comment article was accepted. Both our comments and a response by the original authors were finally published in the April 2022 issue of the journal [3, 4]... which brings us back to the present.
Four main issues were raised in our original comment. In this section, I would like to go through our claims, the response from Verma et al., and my thoughts on that response. The four issues that we raised are:
Let's take them one by one.
This one is very straightforward. In their reply, the authors recognised the error and recomputed the results after correction. Fortunately, they find that "the impact of fixing this bug is small". The increase of .3%-.5% in the overall PQ for most teams with the corrected code [4, Table I] is in line with our own experiments. They also find, as we suspected, that some teams were disproportionately affected ("L8" moves three ranks up to "L5" with a 16% improvement in PQ, "L13" moves three ranks up to "L10" with a 16.5% improvement): this is because the error is particularly strong if the object labels between the "ground truth" and "predictions" are very different (as in: using different ranges of numbers), so it's likely that these teams used a different labelling process (full explanation in our comments [3] or on our Notebook on GitHub).
Here, the authors also admit the error, and issue an amended table for the supplementary materials, so I have no further comments to make.
To our third claim, the authors argue that it comes down to a matter of methodological choice. Quoting from their reply [4, II.C]:
[T]he false positive for one class will be false negative for another class in an mutually exclusive and exhaustive multi-class multi-instance detection problem. We did not want to double count an error, and therefore our loops for error counting run over the ground truth objects. The interpretation of positives and negatives in multi-class problems is a matter interpretation until settled, and this leads to multiple ways of computing the PQ metric for multi-class problems.
I disagree with this for several reasons. To better explain what's going on (the problem, the author's response, and why I think it's wrong), it will be easier to look at a fabricated example. In the figure below, we have a "ground truth" and a "prediction", where colours correspond to classes, numbers to ground truth instance labels, and letters to predicted instance labels.
The submission format require each class' labels to be in a separate file, so in such a situation we would have two "ground truth" label maps (let's call them GT_Blue and GT_Green) and three "prediction" label maps (P_Blue, P_Green and P_White), each containing the labelled mask for one specific class. A pixel cannot belong to two different classes (although there is no mechanism in the code to verify that the submission is valid in this regard).
In the current implementation of the evaluation code, these files would be processed in the following way:
Open GT_Blue and get label map.
Open P_Blue to get corresponding predictions.
Compute PQ_Blue based on GT_Blue and P_Blue.
-> 2 True Positives (1-A, 4-D) and 1 False Positive (C)
Open GT_Green and get label map.
Open P_Green to get corresponding predictions.
Compute PQ_Green.
-> 1 True Positive (5-E) and 2 False Negatives (2, 3)
Stop.
So P_White is never opened, and the False Positive "B" will never be counted. If we look at the full confusion matrix for this image, we should have (with rows corresponding to "ground truth" classes and columns to "predicted" classes:
| No obj | Blue | Green | White | |
|---|---|---|---|---|
| No obj | 0 | 0 | 0 | 1 |
| Blue | 0 | 2 | 0 | 0 |
| Green | 1 | 1 | 1 | 0 |
| White | 0 | 0 | 0 | 0 |
But with the evaluation code as it is written, we end up with:
| No obj | Blue | Green | White | |
|---|---|---|---|---|
| No obj | 0 | 0 | 0 | 0 |
| Blue | 0 | 2 | 0 | 0 |
| Green | 1 | 1 | 1 | 0 |
| White | 0 | 0 | 0 | 0 |
Coming back now to the author's reply, the statement that "the false positive for one class will be false negative for another" is incorrect... unless you count the background "no object" class, which we shouldn't, as the PQ is not computed for the background class. In our fabricated example, the false positive will not be counted at all.
What if the white "B" object had been matched with, for instance, the green "2" object, which at the moment is a "Green False Negative"? Then the "2-B" match would be both a "Green FN" and a "White FP". The idea that, in such case, it should only be counted once, however, would be an important deviation the PQ metric as defined in [5], and it should then be clearly explained in the methods.
As the metric is computed independently for each class, the misclassification should clearly impact both the "Green" class metric and the "White" class metric. In fact, it is the case for other misclassifications, such as the "3-C" match in our fabricated example, which is counted both as a "Green FN" and a "Blue FP". The only time such misclassifications are not counted "twice" in the evaluation code is if there is no ground truth instance of that class in that particular image patch.
This is not a matter of interpretation in this case: it is clearly a mistake. The effect of that mistake can also be very large on the metric. From our experiment on the teams' released "colour-coded" predictions, correcting this mistake led to a drop of 13-15% in the computed PQ. For instance, looking at the SJTU_426 team, we have a 0.4% increase in the PQ when correcting the PQ computation typo (same as the challenge organisers), but we have a massive 14% drop in PQ when we add the missed False Positives:
| SJTU_426 | Challenge eval. | Corr. Typo | Corr. FP | Corr. FP + Typo |
|---|---|---|---|---|
| Verma et al. | 0.579 | 0.618 | - | - |
| Recomputed | 0.554 | 0.594 | 0.424 | 0.454 |
Our replication of the results are based on the "colour-coded" prediction maps. They will be slightly different from the original submission, but should be almost identical in terms of detection performances, which is what changes between those versions of the evaluation code. So while the absolute value is not exactly the same, the delta between the different error corrections should be in the right range.
There is an actual question of interpretation on how exactly those specific false positives should be counted. In our fabricated example, if there was no "White" prediction, then the PQ_white would be undetermined and wouldn't be counted in the average, but if we have a single false positive, we immediately get a PQ of 0 (hence the large impact on the metric). The solution to that problem, however, isn't to just remove the false positives... But to correct the last problem that we have to address: the aggregation process.
There are two parts to the author's reply to our concerns about the aggregation process. The first part is, again, to argue that aggregating "per-patient" (i.e. computing the PQ directly at the patient level and then averaging over the 25 patients of the test set) or "per-patch" (computing the PQ at the image patch level and then averaging over the 101 image patches of the test set) is a methodological choice, and the second is to state that it was clear in their methodology that they chose the second option, so it's not an error on their part that requires a correction but rather a choice that may be discussed in future works.
Concerning the latter, there may indeed have been some confusion which, as they admit, comes from a typing error in their manuscript (where they mention "25 test images" and aggregating "25 PQ_i scores", which correspond to the number of patients and not the number of patches). It led me to the impression that there was simply a certain inconsistency in their naming convention through the paper, where "image" sometimes referred to WSI and sometimes to image patch.
Part of the confusion also comes from their relatively consistent use of the term "sub-image" in the pre-challenge description of the dataset to refer to the image patches. I was regularly consulting that document as well during my analysis, so it made sense to me that "image" would in general refer to "Whole-Slide Image" and "sub-image" to "image patch". As the information in the supplementary materials shows there is only one WSI per patient, this interpretation seemed reasonable.
I can certainly believe that it wasn't their intent, however, and that it was very clear for them (and possibly for the challenge participants) that the PQ was always meant to be computed per-patch in the challenge. So the question becomes: is that a valid methodological choice?
First: what is the problem with computing the PQ "per-patch"? The difference in size between the different patches is enormous, with the smallest image in the dataset having a size of 86x33px, and the largest a size of 1760x1771px, more than a 1000 times larger in number of pixels! The difference in terms of number of ground truth objects is also very large, ranging from 2 to 861 per patch. Even looking at objects of the least frequent class, we can have anywhere between 1 and 15 instances in patches where the class is represented. This means that the cost of making an error on some image patches is orders of magnitudes higher than on others.
The better option that I identified in our comments article was to compute the PQ per-patient. This vastly decreases the size variability, and it also makes sense for a biomedical dataset. Patches taken from the same patient (and particularly, as is the case here, the same WSI) may share some common properties, so that they can't really be considered independent samples. It also increases the number of ground truth objects at the moment where the metric is computed, which avoids the effect of a single False Positive for an object not present in the ground truth immediately setting the PQ to 0, as in our previous example. The distribution of ground truth objects is more likely to be representative on a larger sample, and the PQ will therefore be more less "noisy". Being able to estimate whether a particular algorithm's performances are steady over multiple patients is also very valuable information, so it makes sense to choose that over the other option identified in the author's reply, which is to compute the PQ just once, at the level of the entire dataset.
The main drawback that the authors identify to using the "one PQ on the whole dataset" approach in their reply is that "this approach does not allow for a robust computation of confidence intervals". I'm very unconvinced by this line of reasoning. First of all, it doesn't really say anything about the per-patient proposition (which does allow for confidence intervals, although obviously with less samples these will be larger). Second, there is the aforementioned problem of the samples' independence. Confidence intervals should really be measured at the patient level anyway, as the patient are, in the end, the "samples" that we are studying.
If this is a methodological question, I don't really think it's as open as the author's reply would suggest. In this case, it seems very clear that the per-patient option is better, and I would even say that, given the scale of the "weights" difference given to the errors, the "per-patch" option is in this case even incorrect. It could be justified when the extracted patch are of very similar sizes, but not in this particular dataset.
The corrected results published by Verma et al. in [4] are, in my opinion, still incorrect. The correct ranking of the challenge is, therefore, unknown, and we shouldn't draw any conclusions on the merits of the different methods proposed by the participants. I doubt that the ranking would change by a lot if all corrections were implemented, but as we have seen with the first correction, it's possible that some participants were affected by some of the errors more than others.
While I'm disappointed by the unwillingness of the organisers to directly work with us on correcting the problems, I would like to emphasise that I don't think they did a bad job overall with the challenge. In fact, as I've repeatedly highlighted, their level of transparency on their data and code is higher than any other digital pathology segmentation challenge that I've seen. That's what interested me in their data in the first place, and what allowed us to perform our study on the PQ metric [2].
Organising a successful international competition and compiling such a dataset is a very big achievement, whatever problems may remain in the results. This whole saga also highlight how important it is to increase the transparency in the reporting of challenge results in general. Without the team's predictions and the evaluation code, results are unverifiable and unreplicable. MoNuSAC really went in the right direction here, although they fell short of releasing all participants' results, and released a "visualisation" instead of the raw prediction maps.
What we can see in every challenge that we analyse is that mistakes happen all the time: in the dataset production, in the evaluation methodology, in the code... Challenges are extremely costly and time-consuming to organise, and they use up a lot of resources (from the organisers, but also from the participants). We should really try to make sure that the results that we get from them are accurate. If challenge organisers go for a fully transparent approach to the evaluation process, then the responsibility of checking the validity of the results becomes shared by the whole community, and our trust in these results is improved.
There are also some things in the process with the journal which I think could be improved. First of all, given the nature of the error we found, I think that some form of notice should have been quickly added to the original publication on the journal's website. Between October 2021 and February 2022, there was reasonable doubt about the validity of the results and, since February 2022 and the acceptation of the authors' reply, it is certain that the original results are incorrect.
Even now that the comment and response have been published, there is still no link to those from the original publication, meaning that the original results are likely to be cited without noticing that they have been amended, and that there are additional concerns beyond what was corrected.
I do think that the journal's Editor-in-Chief and Managing Editor were reactive and tried to do things right. The fact that they had to navigate through a process that seemed obscure to everyone is worrying, however. In many ways, "peer-review" starts when the article is published and, therefore, actually available to more than a couple of "peers". Corrections and retractions should be a natural part of the publishing process. Mistakes happen. They only are a problem if they can't be detected and corrected.
Download