[Reading] Reviews of medical image registration

My new project involves a lot of image registration, which is an image analysis task that I haven’t really worked on much before. The goal, in the end, is to be able to “put together” information coming from multiple modalities and taken at different times: CT scans, MRI, and also histology images. This means putting everything into the same frame of reference – a registration task.

So I obviously need to do some reading. As a starting point, we will use three big reviews of medical image registration. The first is a 2014 review (Oliveira and Tavares 2014). I always like to start from reviews from the pre-”deep learning” era when looking at a task that I’m less familiar with, as they generally give a better overview of the general pipeline and the range of possible approaches. To that, I add a chapter from the 2020 “Handbook of Medical Image Computing and Computer Assisted Intervention,” focusing on registration using “machine learning and deep learning” (Cao et al. 2020). The last one, also from 2020, surveys deep learning methods more specifically (Haskins, Kruger, and Yan 2020).

What is image registration

Image registration “can be defined as the process of aligning two or more images” (Oliveira and Tavares 2014). These may come from different modalities (e.g. CT and MRI), different times (e.g. to monitor tumor growth)… They may be 2D images (e.g. successive slices of a tissue block in digital pathology) or 3D images (e.g. MRI volume). (Cao et al. 2020) put it more mathematically as finding the transformation \(\phi^*\) such that:

\[ \phi^*={argmin}_\phi {S(I_R, \phi(I_M))} \]

Where \(I_R\) is the reference image (often called “fixed”), \(I_M\) is the floating image (or “moving”), and \(S\) is a “similarity metric” that measure show well the transformed image \(\phi(I_M)\) matches the reference.

So the main elements that we have to play with are:

• A transformation model
• The similarity metric (how do we define what “matching” means)
• An optimization strategy: how do we minimize \(S\) so that we can find \(\phi^*\).

Transformation models

The transformation model determines how we can modify the moving image. Broadly speaking, we can make a distinction between global models — e.g. rigid or affine transforms — which apply a single operation on the whole “image matrix,” and local or deformable models, which can be expressed as a “deformation field” where each voxel is associated to a vector pointing to its “new” position in the transformed image.

Rigid transforms are often used as a pre-registration step, to broadly align the two images before refining with a more complex and/or local model.

Classic similarity metrics

This is where a lot of the complexity lies – how do you define what counts as a “good match?” It’s particularly difficult in multi-modal problems, where the nature of the information in the two images may be very different. (Oliveira and Tavares 2014) and (Cao et al. 2020) both have mostly the same list of “commonly used” intensity-based metrics:

• Sum of Squared Differences / Mean Squared Differences, which assumes that “the corresponding structures in both images should have identical intensities” (Oliveira and Tavares 2014).
• Correlation Ratio, (Normalized) Cross-Correlation, which assumes that “there is a linear relation between the intensities of the corresponding structures” (Oliveira and Tavares 2014).
• (Normalized) Mutual Information, which assumes that “there is a functional between the variables involved, e.g. between the intensities of both images” (Oliveira and Tavares 2014).

The latter is generally recommended for multimodal registration, as the relationship between the voxel intensities between, for instance, a CT image and a MRI will not be simply linear.

Optimization strategies

Usually — particularly for complex transforms — we’ll have some sort of iterative process such as a gradient descent algorithm. Pre-registration with a rigid transform tends to make the process easier (or, at the very least, faster).

What about machine / deep learning?

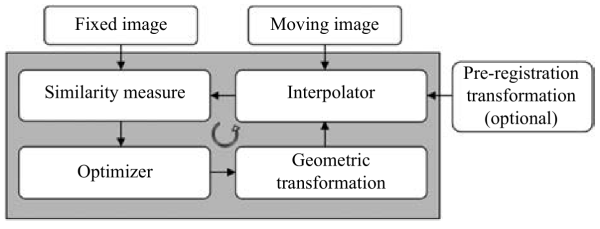
Focusing on the multimodal registration problem, (Cao et al. 2020) and (Haskins, Kruger, and Yan 2020) give us some insights on how/where machine learning can intervene in the process.

• Learning a similarity metric to improve an otherwise classic pipline. The idea is found for instance in a deep learning method proposed in (Cheng, Zhang, and Zheng 2018). A CNN classifier is trained to “learn the correspondence of two image patches,” then the probability at the output of the CNN is used as a similarity score during new registration. An obvious difficulty is that this requires to have well aligned pairs of images as a training set.
• Learning a common feature representation Here the idea is that, since the “intensity values” don’t have the same meaning, we should try to find an “in-between” feature space where the projections from matching features (from both images) are well correlated.
• Learning an appearance mapping model between modalities, e.g. to generate a “pseudo-CT” from an MRI. This then reduces the problem to an easier, monomodal registration problem.
• Fully learning the transformation itself is much more complicated. It may be possible for relatively simple models (e.g. learning the transformation matrix of an affine transform), but for a deformable model the supervision is way too impractical to create.

Evaluation of the results

The evaluation of the results is a particularly difficult problem for registration, and it’s a problem that I’ll probably look into a lot more deeply, as I’ve done for segmentation and classification methods before (Foucart 2022).

As Oliveira notes, “the image similarity measure optimisation can be used as a crude accuracy measure,” but “most similarity measures frequently used have no geometric/physical significance” (Oliveira and Tavares 2014). So the most common approach is to “manually identify a set of corresponding points in both input images (…) and use them to assess the registration accuracy.” This, however, means relying on an expert-provided “ground truth,” with all the problems that come along (this is where I point again to my thesis, I guess!)

He also mentions using the Dice similarity coefficient (which is the “per-pixel” F1 score, in classification/detection terms) to quantify “the amount of overlapping regions.”

Not mentioned but, I think, potentially useful as well in the same vein would be contour-based measures such as the Hausdorff’s Distance, or similar → for instance, using a border detector and then measuring that the main edges in the registered and target image are close to each other.

Conclusions

So that wraps this first look at the state-of-the-art. It’s clear that a key difficulty here is that we have a problem with lots of possible choices and parameters and which is difficult to objectively evaluate or, even, objectively pose. As an example, one of the things we need to do in the project is to register histology slices that are separated by a distance of ~100µm. So the goal is not really to match one image to another: there is no actual “match” between the two, they are different parts of the object. Instead, we are trying to “correctly” place the tissue sections in the slides at their correct position and orientation in a 3D volume — and then register that to a CT image.

Getting a good looking results is one thing, but objectively validating that the results are “correct,” or even defining what “correct” means in this case… will be interesting.

References